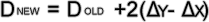Rasterização de Pontos:
Como os sistemas operacionais atuais não permitem que se escreva diretamente na memoria, vamos utilizar um framework disponibilizado pelo professor Christian Azambuja Pagot para simular a escrita no ColorBuffer.
A função PutPixel(): Essa função tem como objetivo "desenhar" um pixel na tela, recebendo coordenadas x e y e cor RGBA (red, green, blue, alpha) . Essa função será necessário na criação das outras funções: DrawLine e DrawTriangle.
A posição do pixel na coordenada x e y é calculada através da seguinte função:
Abaixo temos a função PutPixel com o calculo implementado na variável p, que recebe o valor da posição do pixel no ColorBuffer e o ponteiro FBptr que acessa o pixel do FrameBuffer, que possui 4 bytes, e em cada byte guarda um componente da cor RGBA.
Compilando e executando esse código, temos esse resultado:
 |
| Rasterização da Função PutPixel |
Rasterização de Linhas:
Algorítimo de Bresenham: Esse algorítimo realiza a rasterização de segmentos de reta empregando apenas operações de aritmética de inteiros e , portanto, permite um maior desempenho. Esse algorítimo utiliza o método do ponto médio.
Na figura 1 tem uma linha reta que intersepta duas colunas de pixels. Em cada coluna encontra-se dois pixels que se encontram mais próximos da reta, um abaixo e outro em cima. Se o ponto médio se encontrar em baixo da reta (M2) deverá ser pintado o pixel acima, caso ao contrario (ponto M1) o pixel a ser selecionado será o abaixo da reta.
 |
| Figura 1. |
A função DrawLine(): Função para rasterizar linhas a partir de dois pontos, recebendo dois paramentos de coordenadas dos pixels e dois para as cores. Será utilizado o algorítimo de Bresenham.
As variações de dx e dy terão os seguintes valores:
dx = x2 - x1
dy = y2 - y1
A função da reta tem valor zero para pontos sobre ela, os positivos são os valores acima dela e os negativos abaixo dela. Então temos que fazer o teste do ponto médio, basta calcular a função d e verificar o seu sinal. Para calcular a função d temos:
A partir do valor de d, verifica-se, se d>0 o pixel escolhido será o acima da reta, caso d<0 o pixel será o abaixo dela.
Após verificação do pixel escolhido,agora atualizaremos o valor de d, se o pixel acima da reta foi o ultimo escolhido então a incrementação será apenas no eixo x.
Também temos que verificar o valor inicial de d:
O algorítimo de Bresenham é limitado a apenas um octante. Porém é possível modifica-lo para implementa-lo para os outros octantes da seguinte forma:
Se o ponto médio estiver entre 0 e 1, o d inicial será (d= 2dy -dx), para d>=0 o valor de d será (d+=2(dy-dx) ) e então x++ e y++, caso o d<0 o valor de d será (d+=2dy) e então apenas x++.
Se o ponto médio estiver entre -1 e 0, o d inicial será (d= 2dy +dx), para d>=0 o valor de d será (d+=2dy) e então x++, caso o d<0 o valor de d será(d+=2(dy+dx) ) e então x++ e
y--.
Se o ponto médio for maior que zero, o d inicial será (d= dy - 2dx), para d>=0 o valor de d será (d+=-2dx) e então y++, caso o d<0 o valor de d será(d+=2(dy-dx) ) e então x++ e
y++.
Se o ponto médio for menor que zero, o d inicial será (d= dy + 2dx), para d>=0 o valor de d será (d+=2(dy+dx)) e então x++ e y--, caso o d<0 o valor de d será(d+=2dx ) e então
y--.
Obtive o seguinte resultado:
A partir do valor de d, verifica-se, se d>0 o pixel escolhido será o acima da reta, caso d<0 o pixel será o abaixo dela.
Após verificação do pixel escolhido,agora atualizaremos o valor de d, se o pixel acima da reta foi o ultimo escolhido então a incrementação será apenas no eixo x.
Caso o pixel abaixo da reta foi o escolhido:
Caso o pixel acima da reta foi o escolhido:
O algorítimo de Bresenham é limitado a apenas um octante. Porém é possível modifica-lo para implementa-lo para os outros octantes da seguinte forma:
Se o ponto médio estiver entre 0 e 1, o d inicial será (d= 2dy -dx), para d>=0 o valor de d será (d+=2(dy-dx) ) e então x++ e y++, caso o d<0 o valor de d será (d+=2dy) e então apenas x++.
Se o ponto médio estiver entre -1 e 0, o d inicial será (d= 2dy +dx), para d>=0 o valor de d será (d+=2dy) e então x++, caso o d<0 o valor de d será(d+=2(dy+dx) ) e então x++ e
y--.
Se o ponto médio for maior que zero, o d inicial será (d= dy - 2dx), para d>=0 o valor de d será (d+=-2dx) e então y++, caso o d<0 o valor de d será(d+=2(dy-dx) ) e então x++ e
y++.
Se o ponto médio for menor que zero, o d inicial será (d= dy + 2dx), para d>=0 o valor de d será (d+=2(dy+dx)) e então x++ e y--, caso o d<0 o valor de d será(d+=2dx ) e então
y--.
Obtive o seguinte resultado:
 |
| Rasterização de linha |
Interpolação de Cores:
Foi criada uma função que a partir do primeiro ponto desenhado calcula a distancia desse ponto ate o ponto final, e outra função que recebe a divisão entre a distância parcial(distP) com a distancia total(distT) e as cores inicial(cor1) e final(cor2), e essa porcentagem (p) será multiplicado pela cor do ponto inicial, somado a esse p subtraído por 1 e multiplicado pelo valor da cor final, retornando a nova cor do ponto final, esse processo será repetido para cada pixel desenhado ate chegar ao pixel final.
O calculo da distância entre dois pontos é feita a partir da seguinte equação:
e para descobrir a cor do ponto p é através da seguinte equação:
Abaixo você pode conferir uma linha com interpolação de cores:
Rasterização do Triângulo:
A função DrawTriangle(): É uma função bem simples que recebe três vértices que forma um triângulo, como já foi criado funções para rasterização de pontos e linhas, basta apenas chamar a função DrawLine() três vezes. Abaixo está o resultado dessa função:
 |
| Rasterização do Triângulo |
Principais Dificuldades: A maior dificuldade foi na implementação do algorítimo de Brasenham.
Referências Bibliográficas:
<http://pt.wikipedia.org/wiki/Algoritmo_de_Bresenham>Acesso 4 de Março.
<http://www.sabereletronica.com.br/artigos/2605-algoritmo-de-bresenham-o-uso-de-microcontroladores-para-traar-retas-em-lcds> Acesso em 4 de Março.
<http://disciplinas.ist.utl.pt/leic-cg/textos/livro/Rasterizacao.pdf> Acesso em 6 de Março.